На основную страницу кафедры ВТМГБ.
В рамках данного раздела представлены задачи, которые предлагались студентам кафедры ВТМГБ в 2021 году в качестве возможной темы НИР.
2. Развитие INMOST – программной платформы для распределенного математического моделирования >>
3. Моделирование многофазной фильтрации в задачах нефтедобычи >>
4. Моделирование сердечно-сосудистой системы >>
5. Биомеханическое моделирование плечевого и коленного суставов >>
6. Разработка и внедрение алгоритмов компрессии и декомпрессии океанологических данных на основе тензорных разложений >>
7. Разработка версии ИВС “Черное море – ИВМ РАН” для интеграции с Информационной системой Центра коллективного пользования Института космических исследований >>
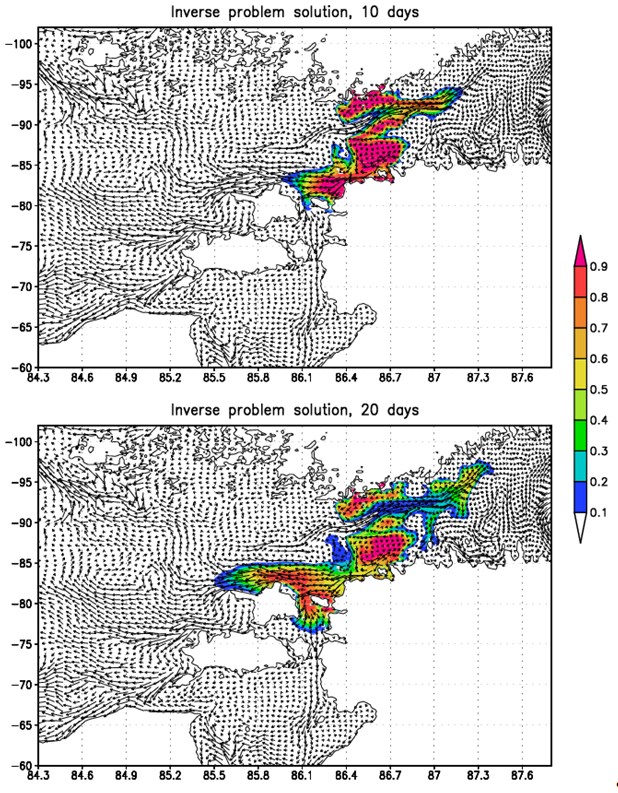
8. Задача о локальных источниках и локальных наблюдениях >>
9. Агентные модели в эпидемиологии >>
10. Математическое моделирование иммунной системы >>
11. Численный анализ устойчивости физических, технических и биологических систем >>
12. Субсезонный и долгосрочный прогноз аномалий погоды >>
13. Cоздание глобальной модели атмосферы для системы прогноза погоды нового поколения >>
14. Система прогноза состояния морского льда Северного Ледовитого океана >>
15. Вычислительная линейная алгебра >>
16. Моделирование климата >>
17. Численное моделирование геофизической турбулентности >>
18. Экспериментальная математика >>
19. Математическое моделирование верхней атмосферы и ионосферы Земли >>
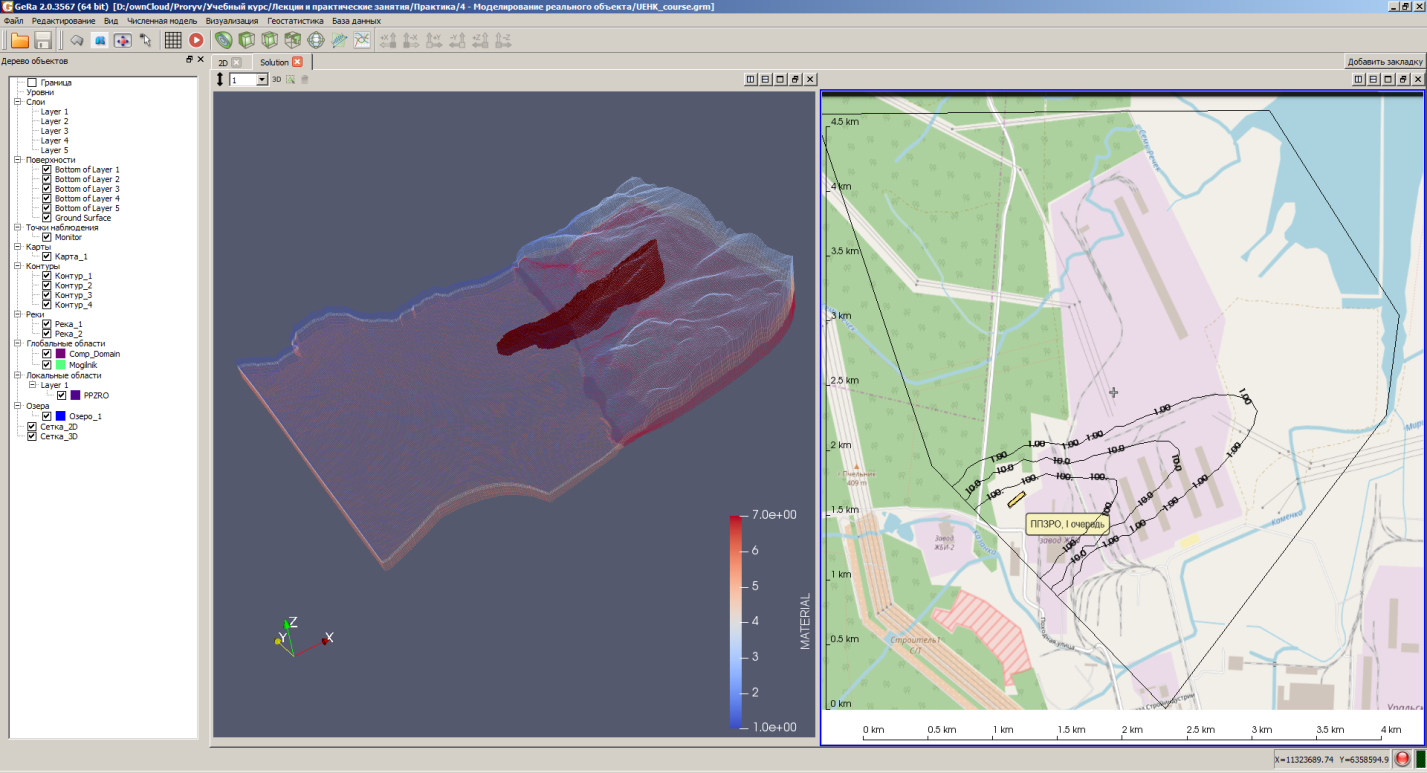
Численное моделирование фильтрации и переноса загрязнений в подземных водахНаучный руководитель к.ф.-м.н. Капырин И.В., Работы направлены на создание вычислительных технологий оценки радиационной и экологической безопасности различных объектов с точки зрения потенциального загрязнения грунтовых вод. Актуальность тематики объясняется становлением новой системы обращения с радиоактивными отходами, предполагающей их обязательное окончательное безопасное захоронение. Также в настоящее время происходят коренные изменения в обращении с отходами производства и потребления, предполагающие реабилитацию загрязненных территорий и создание новых высокотехнологичных полигонов. Для решения этих задач разрабатываются математические модели соответствующих физических и химических процессов, а также численные методы, их реализующие. Основным результатом на сегодняшний день стало создание расчетного кода GeRa, аттестованного для использования при обосновании безопасности объектов использования атомной энергии и применяемого рядом организаций атомной отрасли для решения практических задач. Код GeRa предназначен для моделирования процессов фильтрации и переноса загрязнений в подземных водах, использует современные методы дискретизации на неструктурированных трехмерных сетках и параллельные вычислительные алгоритмы. Студентам в рамках данной тематики исследований предлагаются работы по созданию математических моделей и численных методов моделирования процессов подземной фильтрации и переноса загрязнений в подземных водах. Примеры: перенос со сложными химическими взаимодействиями, миграция примесей в коллоидной форме, тепловая и плотностная конвекция растворов, фильтрация и перенос в трещиновато-пористых средах. Работы сопряжены с решением практических задач для реальных объектов – пунктов захоронения радиоактивных отходов, загрязненных территорий, свалок ТБО. |
|
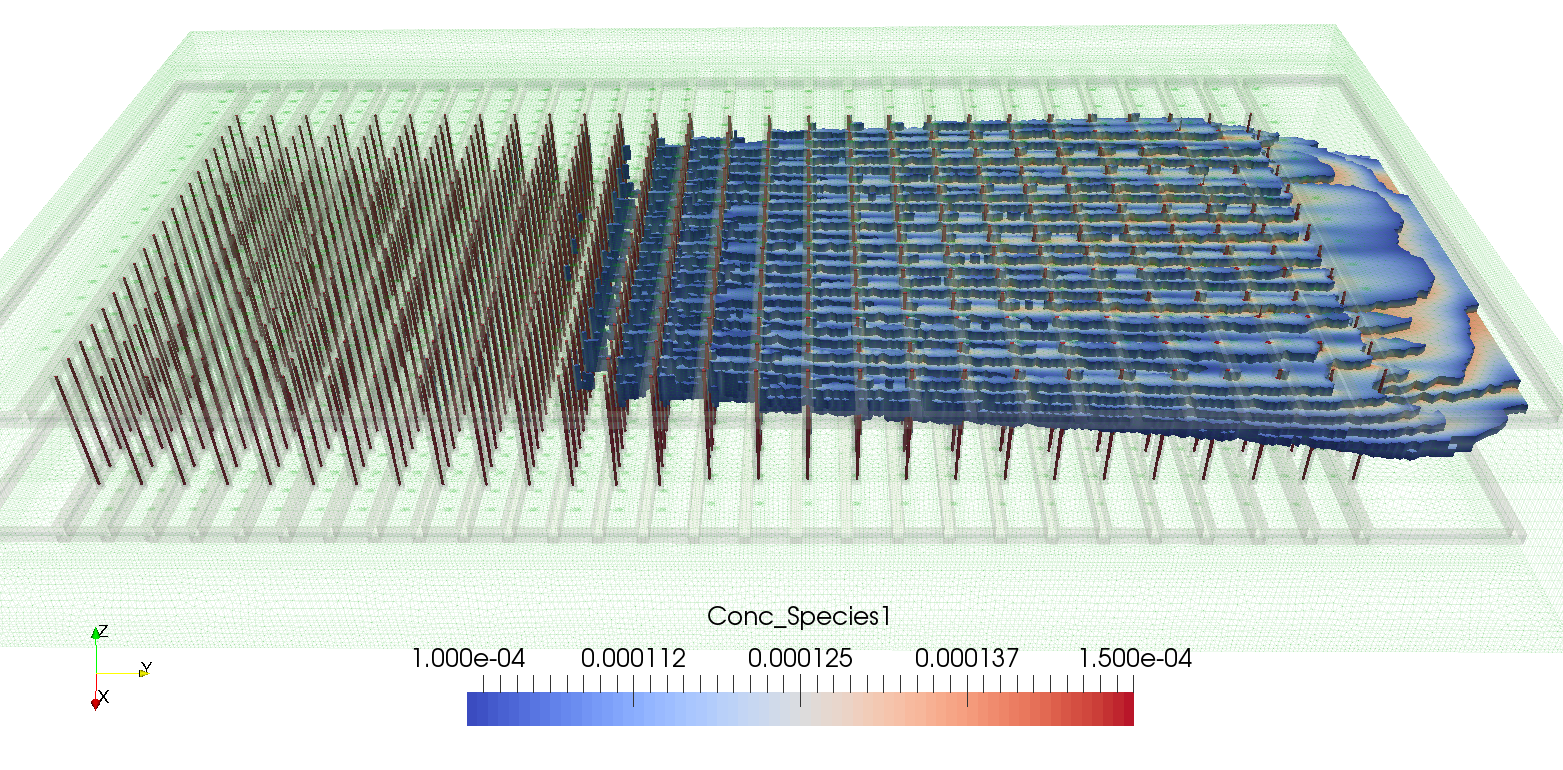
Развитие INMOST – программной платформы для распределенного математического моделированияНаучный руководитель к.ф.-м.н. Терехов К.М., к.ф.-м.н. Коньшин И.Г., Главной задачей программной платформы INMOST является обеспечение пользователя всеми необходимыми средствами для создания и исследования различных численных моделей. В данный момент INMOST является основой для ряда программных комплексов связанных с решением задач математической физики, от моделирования нефтедобычи и оценки загрязнения окружающей среды радионуклидами до движения крови в сосудах и моделирования тромбообразования. В программный комплекс входят как работа с распределенными по процессорам неструктурированными сеточными данными, но и удобный интерфейс для формирования и дальнейшего решения систем линейных уравнений, а также средства визуализации полученного решения. В качестве студенческих проектов предлагается дальнейшее развитие INMOST, а также создание программных комплексов для решения новых задач. Примеры задач: Все задачи имеют прикладное значение. Работы выполняются при поддержке Российского Научного Фонда (РНФ), Российского Фонда Фундаментальных Исследований (РФФИ). |
|
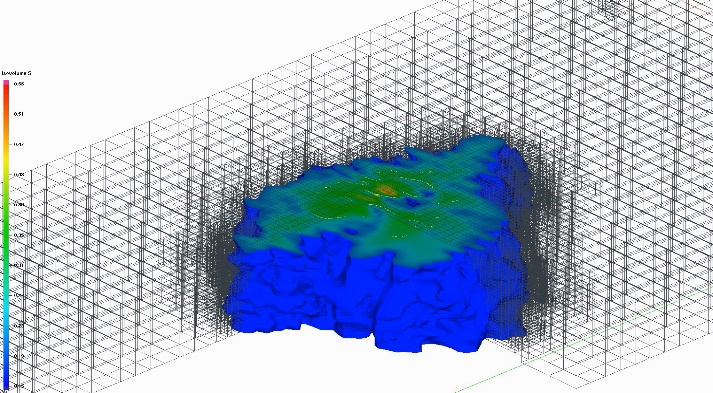
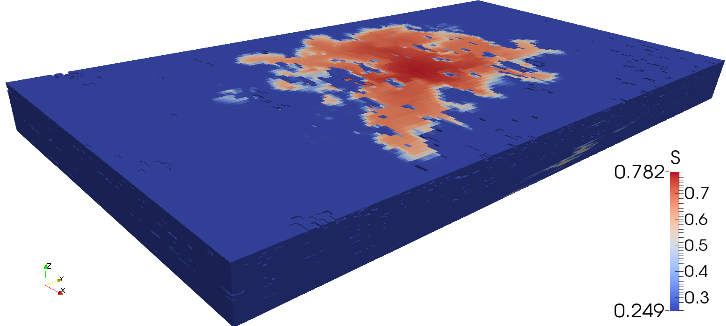
Моделирование многофазной фильтрации в задачах нефтедобычиКонтакты: Математическое моделирование процессов многофазной фильтрации является неотъемлемой частью планирования разработки нефтегазовых месторождений и используется для принятия таких решений, как размещение скважин, проектирование поверхностных сооружений и разработка оперативных стратегий для достижения максимального коэффициента извлечения нефти при минимальных затратах. Использование современных численных методов позволяет повысить как точность, так и скорость получения прогноза, и как следствие – его практическую ценность. В качестве студенческих проектов предлагается развитие разработанного в ИВМ РАН исследовательского гидродинамического симулятора, а также проведение численных экспериментов для конкретных сценариев. Примеры задач: 1. Изучение методов улучшения сходимости для задач трехфазной фильтрации (система вода-нефть-газ), 2. Подготовка и проведение экспериментов для трехфазной фильтрации для конкретных месторождений, 3. Исследование эффектов, возникающих при фазовых переходах, 4. Развитие методов для корректного учета гравитации в задачах фильтрации. Все задачи имеют прикладное значение. Работы выполняются при поддержке Российского Научного Фонда (РНФ) и корпорации ExxonMobil. |
  |
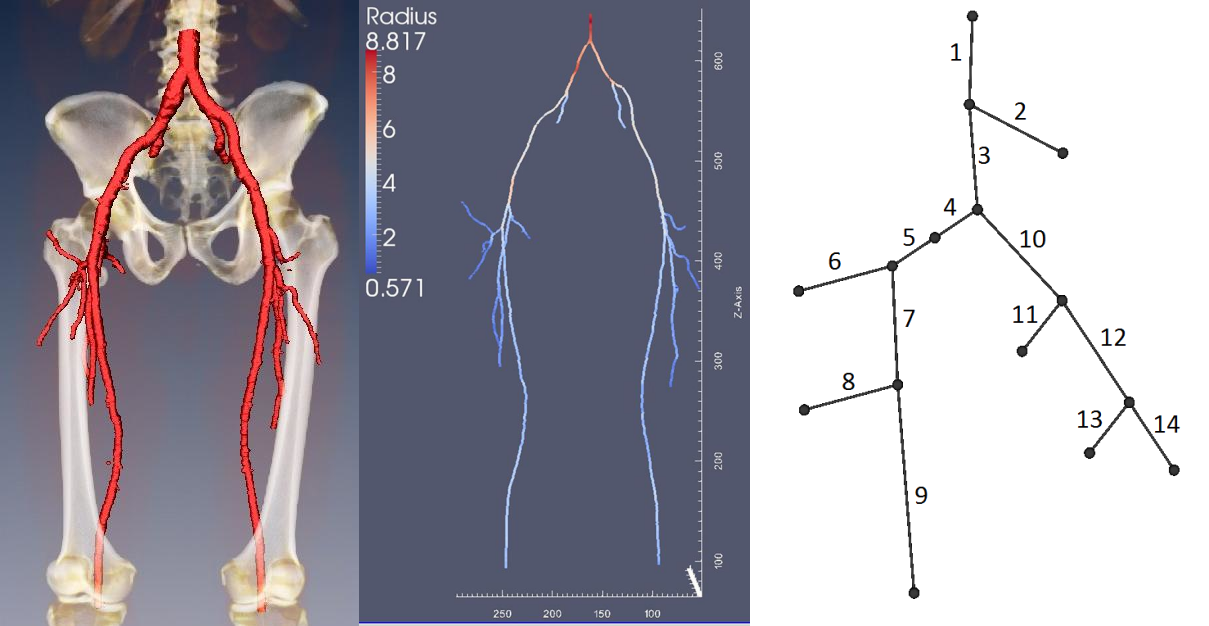
Моделирование работы сердца и его отдельных элементовКонтакты: Заболевания сердечно-сосудистой системы являются основной причиной смертности в мире. В Первом московском государственном медицинском университете (Сеченовском университете) проводятся массовые операции по реконструкции аортального клапана и стентированию коронарных, брахиоцефальных и бедренных артерий. Использование персонализированных математических моделей сердца и кровеносных сосудов при планировании операций повышает их эффективность. ИВМ РАН совместно с Лабораторией математического моделирования в медицине Института персонализированной медицины НТПБ Сеченовского университета разрабатывает модели для вышеприведенных операций, https://dodo.inm.ras.ru/research/rsf-14-31-00024 Кроме того, в рамках сотрудничества ИВМ РАН и Национального медицинского исследовательского центра сердечно-сосудистой хирургии им. А.Н. Бакулева будет разрабатываться персонализированная математическая модель потоков крови для одножелудочковой коррекции врожденных пороков сердца у детей (операции Фонтена) на дооперационном этапе. В качестве студенческих проектов предлагается участие в разработке этой модели, исследованиях на их основе и их внедрении в клиническую практику.” |
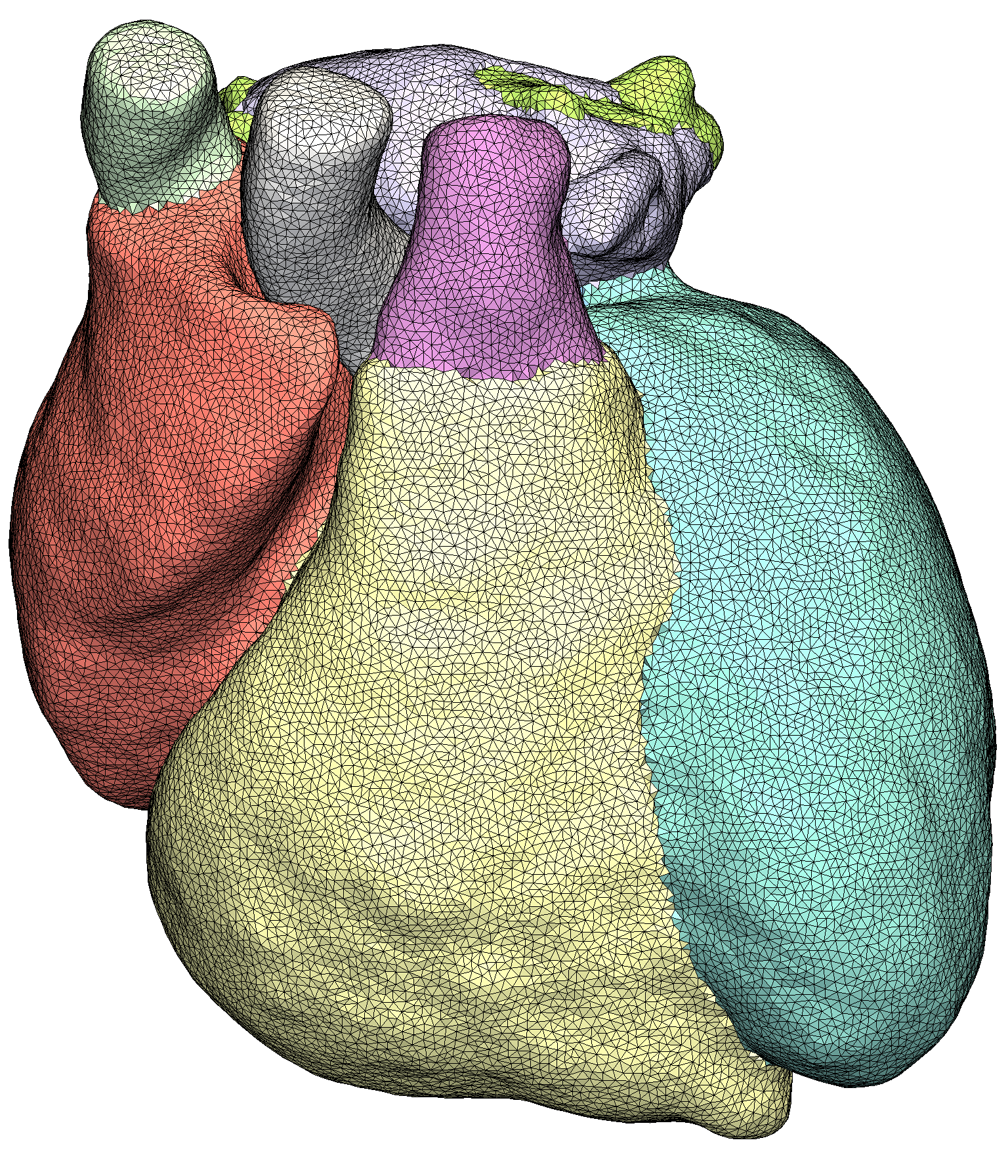 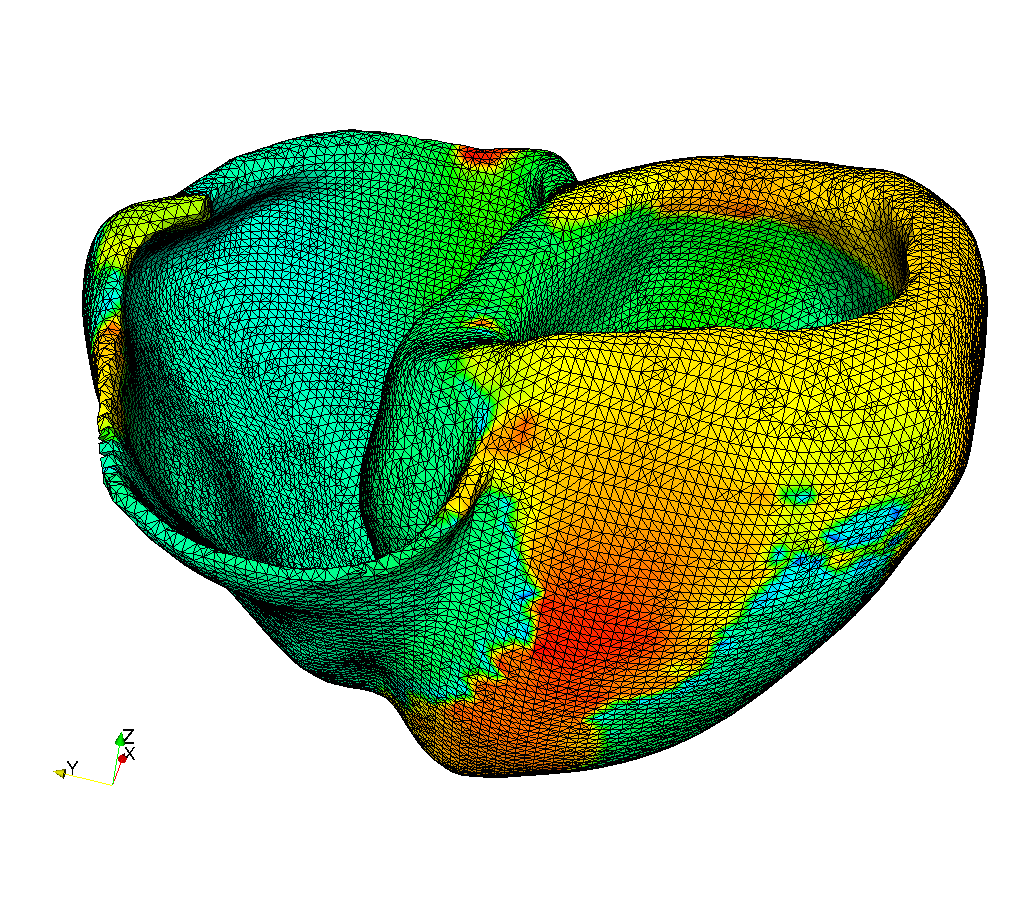 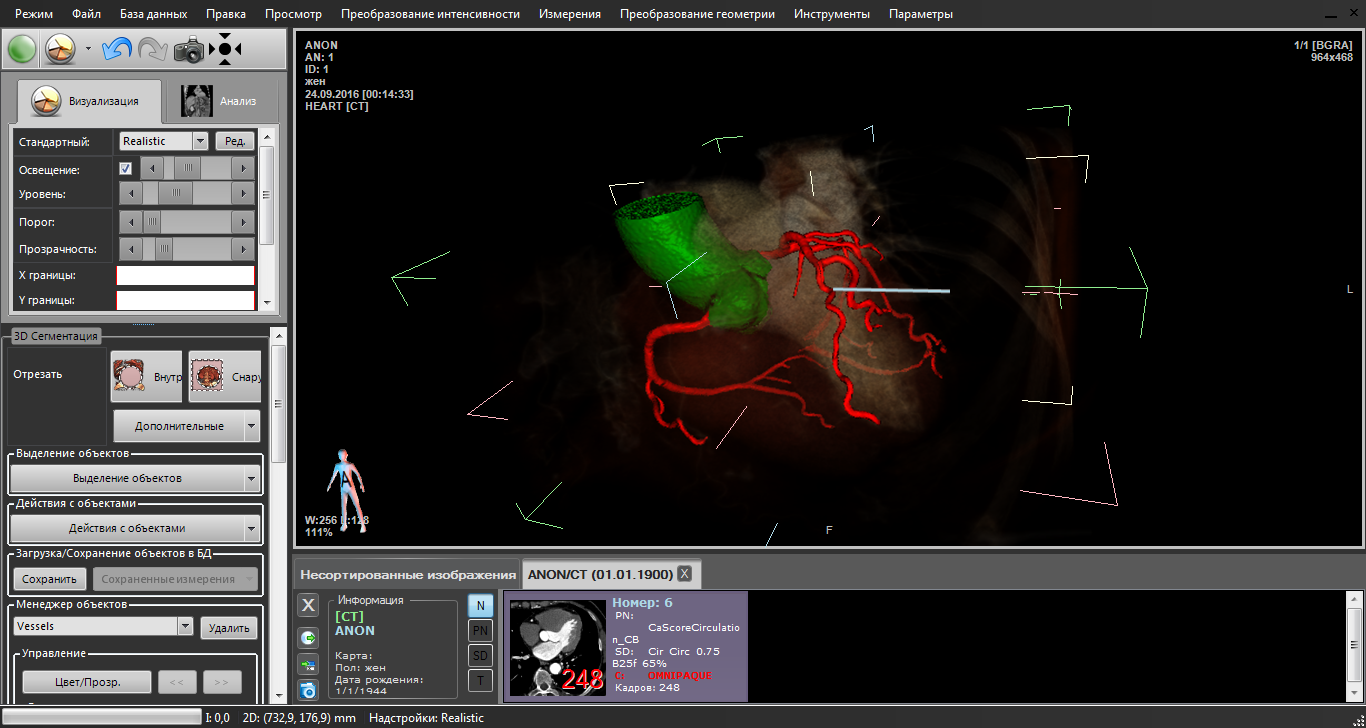 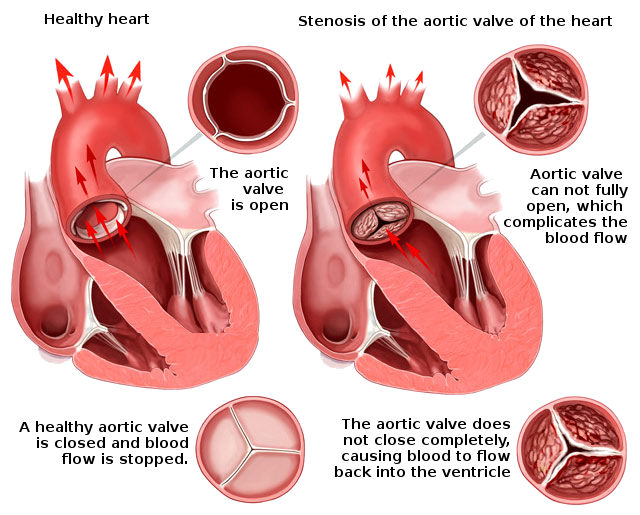   |
Биомеханическое моделирование плечевого и коленного суставовКонтакты: Фундаментальные биомеханические исследования в области травматологии и ортопедии и предсказательное моделирование ортопедических операций являются основой В качестве студенческих проектов предлагается участие в разработке этой модели, исследованиях на их основе и их внедрении в клиническую практику.” |
|
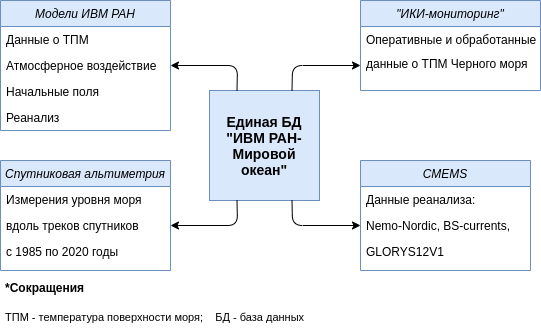
Разработка и внедрение алгоритмов компрессии и декомпрессии океанологических данных на основе тензорных разложенийКонтакты: Исследование предполагает работу с геофизическими данными. Необходимо разработать процедуры сжатия (для хранения на серверах) и восстановления (для последующего использования) геофизических данных различных типов. Работы включают в себя: 1. Разработку процедур сжатия и восстановления временных рядов измерений уровня моря с использованием известных алгоритмов компрессии и декомпрессии на основе тензорных разложений. Исследование вопроса потери данных и фильтрации “шума”. 2. Разработку алгоритмов компрессии и декомпрессии среднесуточных данных наблюдений о состоянии морских акваторий. Применение разработанных алгоритмов для данных, полученных в результатам работы численной модели гидротермодинамики морских акваторий. 3. Применение разработанных алгоритмов для оперативных данных наблюдений, покрывающих часть выбранной акватории. Исследование вопроса потери данных. 4. Внедрение эффективных алгоритмов в Единую базу данных “ИВМ РАН-Мировой океан”. |
|
Разработка версии ИВС “Черное море – ИВМ РАН” для интеграции с Информационной системой Центра коллективного пользования Института космических исследованийКонтакты: Исследование предполагает работу с геофизическими данными и численной моделью гидротермодинамики Черного и Азовского морей и состоит из решения следующих задач: |
|
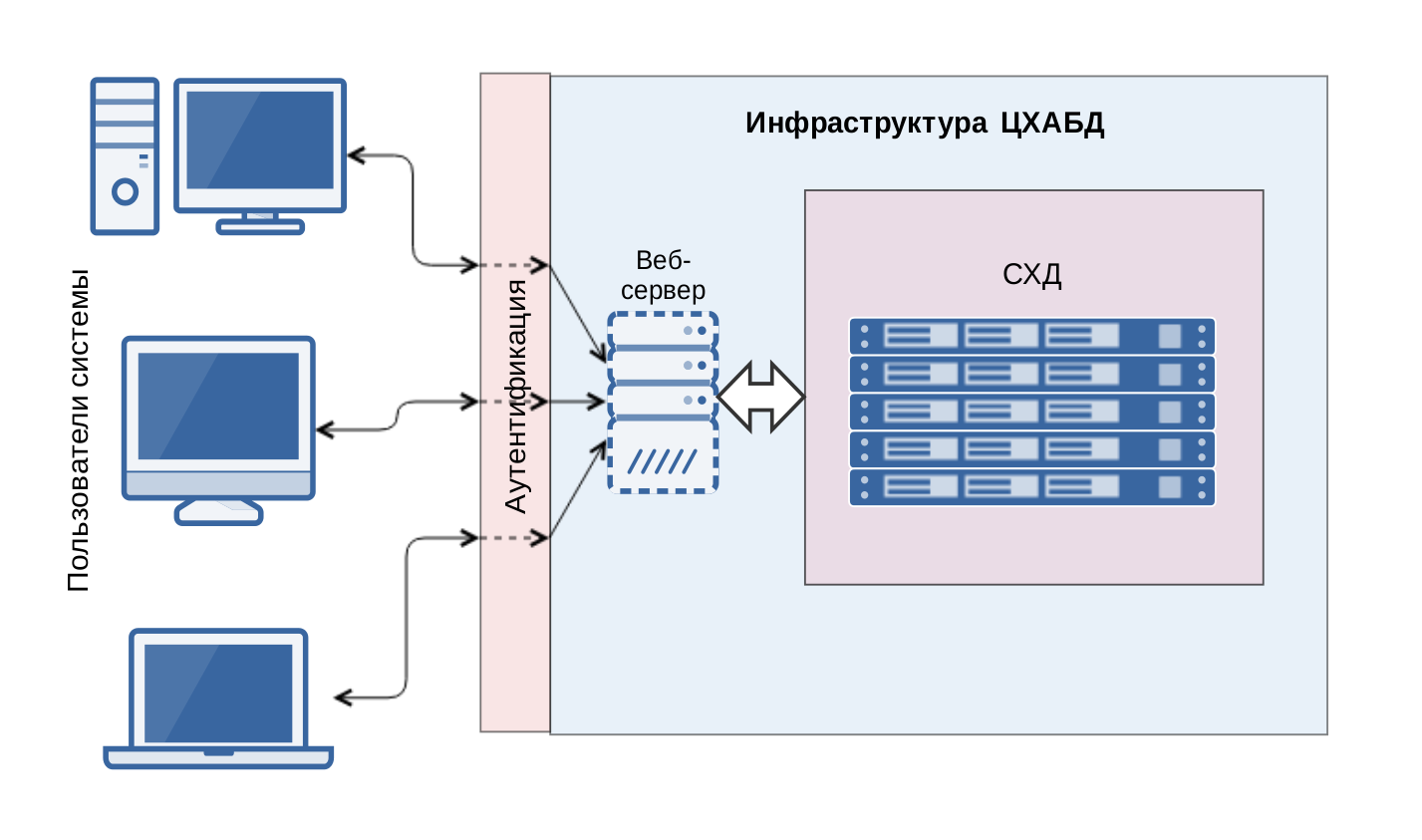
Задача о локальных источниках и локальных наблюденияхКонтакты: Исследование предполагает решение проблемы определения местоположения источника загрязнения при наличии локальных данных наблюдений с датчиков, регистрирующих концентрацию примесей в исследуемом бассейне. Исследование включает в себя решение следующих задач: 1. Дифференциальная постановка задачи о распространении примеси и ее исследование. 2. Постановка задачи оптимального управления (обратной задачи). 3. Разработка численного алгоритма и написание программы для решения задачи. 4. Проведение численных экспериментов. Работа будет проводиться в рамках проекта с Центром хранения и анализа больших данных при МГУ (ЦХАБД МГУ) |
|
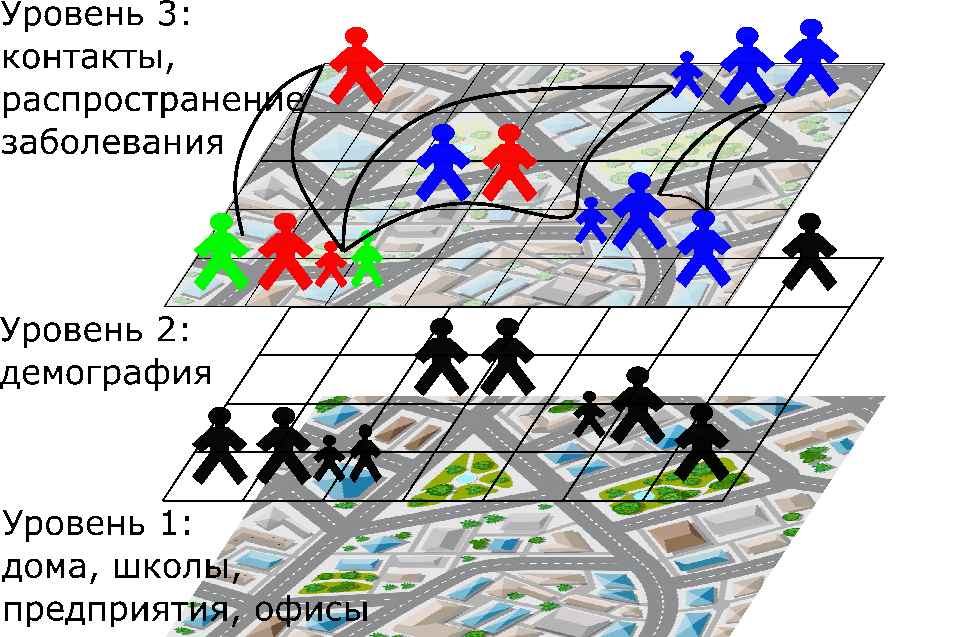
Агентное моделирование распространения вирусной инфекции в городских условияхКонтакты: Агентное моделирование является современным и эффективным методом описания эпидемиологических процессов. Исследования последних лет, посвящённые эпидемиологии вирусных заболеваний, показали несостоятельность моделей, описывающих динамику средних по популяции показателей. Современные вычислительные мощности позволяют моделировать поведение и иммунные характеристики отдельных индивидов или, другими словами, агентов. В нашей группе разработана и в настоящий момент тестируется агентная модель распространения вирусной инфекции в мегаполисе с числом агентов 10 млн. Эту модель предполагается использовать для описания эпидемических процессов в Москве, Санкт-Петербурге, Казани и в других городах с населением более 1 млн. В рамках исследования эпидемиологии вирусных заболеваний на территории Российской Федерации необходимо перейти к городам меньшего размера. Агентная модель города с населением менее 200 тыс. не может быть получена из модели мегаполиса простым уменьшением числа агентов, поскольку нужно учитывать не только отличия в транспортной системе города, но и иной бюджет свободного времени и иную сеть контактов агентов. Студентам предлагается изучить принципиальные отличия популяций небольших городов от популяций мегаполисов и реализовать агентную модель распространения респираторной вирусной инфекции в таком городе. |
 |
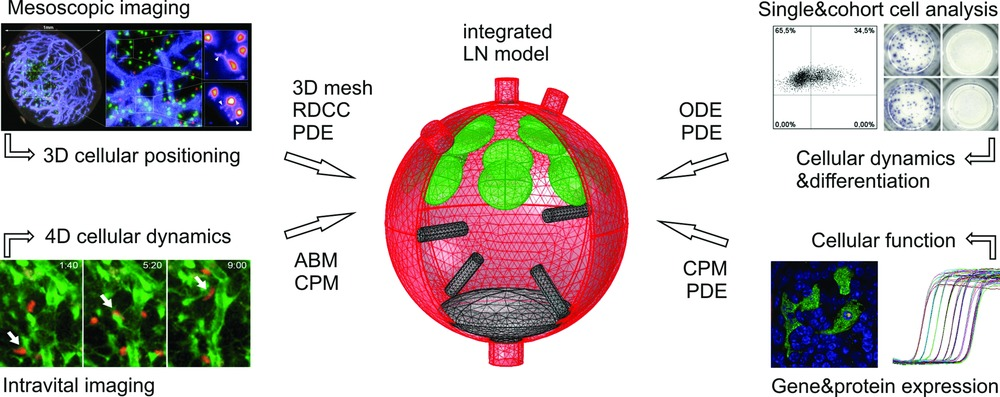
Математическое моделирование иммунной системыКонтакты: Современная иммунология, при анализе механизмов многофакторных заболеваний человека разнообразной природы (ВИЧ, COVID-19, гепатит, грипп и др.), в основе которых лежат процессы иммунной системы, и решении задачи прогнозирования их динамики сталкивается с целым рядом фундаментальных проблем. К ним относятся – высокая размерность пространства состояний системы, многовариантность режимов динамики патологических процессов, нелинейности регуляторных сетей, гетерогенность и вариабельность популяций клеток врожденного и адаптивного иммунитета. Их решение связано с разработкой и применением математических и компьютерных инструментов моделирования иммунных процессов, на основе которых проводится численное исследование траекторий динамики детерминистических, стохастических и гибридных моделей мульти-физических процессов иммунных реакций, геометрическое 3D моделирование структур лимфоидных органов и тканей, ассимиляция экспериментальных и клинических данных, анализ чувствительности и регуляторных контуров различного уровня, решения задач прогнозирования и оптимального управления. В качестве НИР студентам предлагается участие в решении следующих задач: • интегративное мульти-физическое рассмотрение иммунных реакций (физические, молекулярно-биологические и клеточно-популяционные процессы), • выделение топологической структуры клеточных и молекулярных сетей регуляции в норме и при иммуно-зависимых заболеваниях, • использование систем с распределенными параметрами в пространстве фенотипических и физических признаков, • разработка графовых и твердотельных геометрических моделей органов иммунной и лимфатической системы, • идентификация законов управления иммунными процессами в категориях иерархических децентрализованных систем автоматического регулирования. |
 |
Численный анализ устойчивости физических, технических и биологических системНаучный руководитель д.ф.-м.н. Нечепуренко Ю.М., комната 638, yumnech at yandex.ru Возможные направления работы: – Разработка и анализ матричных численных методов исследования устойчивости. – Исследование устойчивости до, транс, сверх и гиперзвуковых аэродинамических сдвиговых течений и анализ ламинарно-турбулентного перехода в них. – Исследование устойчивости стационарных и периодических решений моделей динамики вирусных инфекций и разработка новых алгоритмов терапии. По всем направлениям будет предложены и обсуждены со студентом конкретные задачи, из которых он/она сможет выбрать себе тему научной работы. При этом, возможен как уклон в сторону математики, так и более глубокое погружение в выбранное приложение. Для представления о направлениях исследований прилагаются по одной публикации коллектива по каждой из этих тем. Computing humps of the matrix exponential Excitation of unsteady Görtler vortices by localized surface nonuniformities Maximum response perturbation-based control of virus infection model with time-delays |
|
Субсезонный и долгосрочный прогноз аномалий погодыНаучный руководитель к.ф.-м.н. Фадеев Р.Ю., комната 603, rost.fadeev at gmail.com Глобальная модель атмосферы ПЛАВ разработана в ИВМ РАН и Гидрометцентре России. Сейчас ПЛАВ применяется в Гидрометцентре России для оперативного среднесрочного (от 1 до 10 дней) прогноза погоды, субсезонного (от 10 дней до 1 месяца) и долгосрочного (до 4 месяцев) прогноза аномалий погоды. Возможные темы НИР: 1. Исследование физики дальних связей в атмосфере и их воспроизводимости в рамках модели ПЛАВ. В метеорологии под дальними связями (teleconnection), обычно, понимают нелокальный отклик атмосферы на резкие региональные изменения характеристик поверхности. Это один из важнейших источников предсказуемости на субсезонном и долгосрочном масштабах времени. Описание таких механизмов в рамках численной модели ПЛАВ важно, например, для повышения точности прогноза явлений атмосферного блокирования. 2. Участие в разработке совместной модели атмосфера-океан-морской лед для перспективной системы долгосрочного прогноза погоды. Практически все ведущие метеорологические центры мира за исключением Гидрометцентра России перешли на совместные модели для субсезонного и долгосрочного прогноза аномалий погоды. В России такая модель также реализована (Fadeev et al, 2019, 2018). Сейчас ведутся работы по доведению этой модели до состояния, готового к внедрению в оперативную практику. Задач – много, как и акцентов: физика, программирование, интерпретация результатов. 3. Моделирование снежного покрова в модели ПЛАВ. Характеристики снежного покрова играют важную роль при описании процессов на поверхности (в переходные сезоны, особенно). Внедрение в ПЛАВ усовершенствованной модели снежного покрова позволит повысить точность описания приземных характеристик атмосферы (температуры, прежде всего) и, таким образом, качество прогноза погоды. Конкретная формулировка НИР обсуждаема и может быть скорректирована с учетом интересов студента. |
|
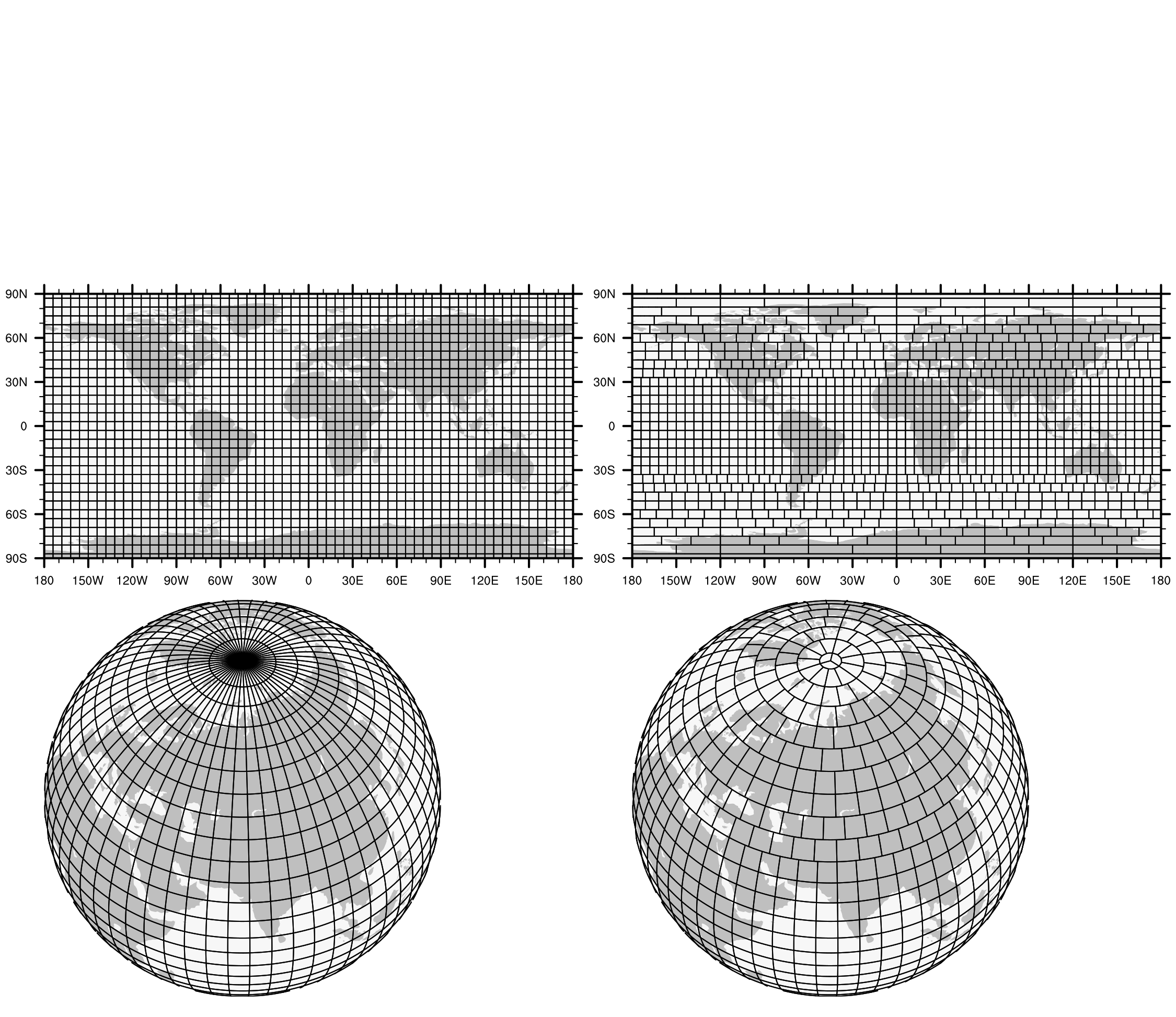
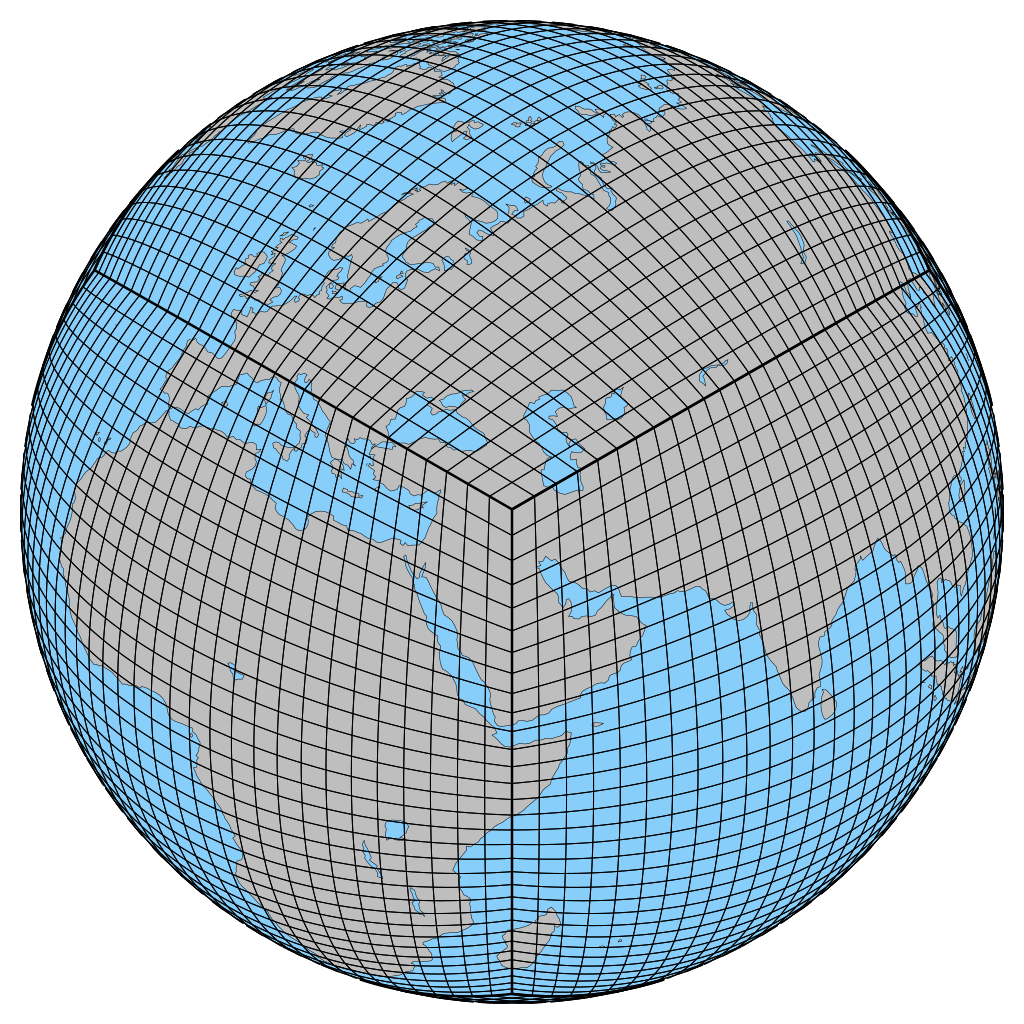
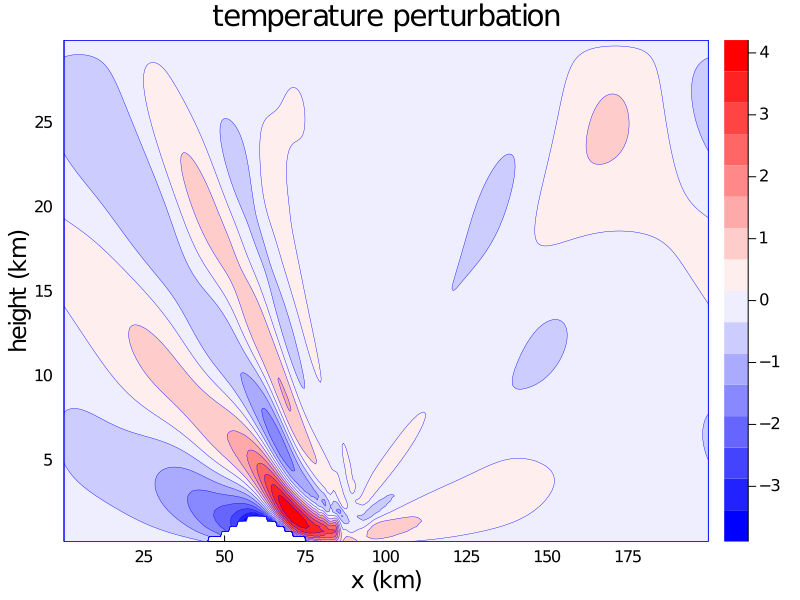
Cоздание глобальной модели атмосферы для системы прогноза погоды нового поколенияНаучный руководитель к.ф.-м.н. Шашкин В.В., комната 603, vvshashkin at gmail.com На сегодняшний день большая часть научных групп, занимающихся моделированием атмосферы и прогнозом погоды, готовятся к переходу на использование глобальных моделей прогноза погоды с очень подробным пространственным разрешением (3-7 км). Такое разрешение позволит модели воспроизводить не только крупномасштабные атмосферные движения, но и ряд локальных эффектов (фронты, шквалы, горные волны), которые обуславливают значительную При переходе к глобальному прогнозу погоды с разрешением 3-7 км, как правило, требуется разработка новой модели атмосферы (модели нового поколения). Это связано с тем, что при подобном пространственном разрешении возникает ряд требований алгоритмам и методам, не свойственных моделям предыдущего поколения: – Высокое быстродействие и параллельная эффективность алгоритмов и численных методов. Возможные задачи студенческих дипломных работ: – Моделирование обтекания горного рельефа с использованием метода погруженных границ. В рамках данной задачи студенту предлагается реализовать и исследовать метод численного решения упрощенных уравнений динамики атмосферы с использованием метода погруженных границ для моделирования обтекания рельефа. В дальнейшем рассматривается возможность внедрения данного метода в полную модель атмосферы. – Разработка и исследование свойств горизонтальных аппроксимаций дифференциальных операторов на сетках с квазиравномерным разрешением на сфере. В рамках данной задачи студентам предлагается исследовать свойства (как численно, так и аналитически) схем пространственной дискретизации для сеток на сфере специального вида (кубическая сфера, редуцированная широтно-долготная сетка) в рамках упрощенных двумерных уравнений динамики атмосферы. Результат данного исследования позволит выделить наиболее перспективные схемы для использования в новой модели атмосферы. – Реализация эффективных параллельных алгоритмов численного решения системы уравнений динамики атмосферы. В частности, предлагается заняться разработкой и исследованием параллельных свойств методов решения систем линейных уравнений с большой разреженной матрицей (многосеточные методы, методы Крылова и другие), возникающих в результате дискретизации уравнений динамики атмосферы. В рамках выполнения данной задачи предполагается работа с одним из самых мощных суперкомпьютеров в России (вычислительная система ГВЦ Росгидромета). |
    |
Система прогноза состояния морского льда Северного Ледовитого океанаНаучный руководитель д.ф.-м.н. Яковлев Н.Г., комната 605, nick_yakovlev at mail.ru В настоящее время в ИВМ РАН начата работа по созданию новой системы краткосрочного прогноза состояния морского льда в Северном Ледовитом океане высокого пространственного разрешения на неструктурированных и адаптивных сетках. Необходимость создания такой системы обусловлена двумя факторами: возросшими требованиями к прогнозу характеристик морского льда на срок до недели, и значительно улучшенными возможностями дистанционного зондирования ледового покрова со спутников. В качестве студенческих проектов предлагается: 1. Реализация улучшенной модели одномерной термодинамики морского льда на графических платах (разработка на языке C с использованием CUDA), с последующим соединением ее с моделью дрейфа льда. Построенная реализация будет использована также в перспективной модели Мирового океана – части новой модели климата Земли. 2. Подключение к разработке динамического ядра модели с использованием библиотеки INMOST на языке программирования C++. Сравнение результатов с полями Европейского прогноза TOPAZ-4. 3. Изучение современных методов дистанционного зондирования состояния льда из космоса и использование соответствующих данных большого объема в системе прогноза, вопросы эффективной численной реализации на параллельных компьютерах. Специфика работы предполагает взаимодействие как со специалистами в различных областях геофизической гидродинамики и вычислительной математики из ИВМ РАН, так и со специалистами в таких областях, как спутниковые системы дистанционного зондирования и физика морских льдов. Помимо чисто кабинетной работы возможно участие в морских экспедициях и в работе студенческой научной школы на архипелаге Шпицберген с полевыми работами по изучению морского льда. |
   |
Вычислительная линейная алгебраНаучный руководитель Академик РАН, проф., д.ф.-м.н. Тыртышников Е.Е., комната 704, eugene.tyrtyshnikov at gmail.com 1. Интерполяционные алгоритмы при решении интегральных уравнений. При дискретизации интегральных уравнений на равномерной сетке обычно возникают матрицы специального вида (многоуровневые теплицевы матрицы), для которых известны быстрые алгоритмы умножения на вектор. В современных итерационных методах решения систем линейных алгебраических уравнений именно эта операция определяет вычислительную сложность каждой отдельной итерации. В ряде практически интересных задач, однако, необходимо применять неравномерные сетки. Цель исследования – построить быстрые алгоритмы умножения матрицы на вектор и в этом случае и применить их для решения объемных интегральных уравнений, возникающих в задачах электродинамики [А.Б.Самохин, Е.Е.Тыртышников. Численный метод решения объемных интегральных уравнений на неравномерной сетке. ЖВМ и МФ, том 61, номер 5 (2021), сс. 189–195]. 2. Редукция моделей и обучающих выборок в задачах машинного обучения. Мы постоянно имеем дело с отображениями, действие которых известно только на некоторой части точек их области определения. При этом есть желание понять, как они действуют в других точках. Обычно выбирается некоторая модель отображения с набором параметров, которые определяются с помощью методов машинного обучения. Одна из главных реальных проблем заключается в том, что для обучения необходимо использовать слишком много точек. Есть две идеи о том, как сократить число точек обучения. Во-первых, можно из всего множества точек обучения выбирать наиболее значимые. Во-вторых, можно попытаться редуцировать саму модель, сократив число ее параметров и, как следствие, число обучающих точек. Цель исследования – посмотреть, как эти идеи работают в задачах прогнозирования значений временных рядов по начальному отрезку времени, изучить современные статистические модели и возможности применения тензорных разложений для их эффективной реализации. 3. Как решать операторные уравнения в случае операторов с коэрцитивно расщепляемой главной частью. Теория сходимости проекционных методов (методов Галеркина) для решения линейного операторного уравнения обычно предполагает выполнение двух условий: (а) аппроксимации для проекторов и (б) коэрцитивности для исходного оператора. Замечательно, что компактное возмущение оператора сохраняет сходимость. Однако есть задачи (например, знаменитое уравнение электрического поля в электродинамике), в которых 4. Применение тензорных разложений при решении кинетических уравнений. Традиционно при решении уравнений Больцмана и уравнений Смолуховского используются стохастические методы, так как классические сеточные методы представляются катастрофически затратными. Совсем недавно для уравнений Больцмана и схожих популяционных уравнений удалось получить эффективные квазисеточные методы, в основе которых лежат традиционные сеточные методы и специальные тензорные представления решения и ядра. Цель исследования – посмотреть, как эти конструкции могут использоваться при решении уравнений Больцмана. 5. Принцип максимального объема в задачах оптимизации. Принцип максимального объема в задачах малоранговой аппроксимации матриц дает замечательный рецепт для выбора малого числа строк и столбцов – креста, по которому матрица восстанавливается с гарантированной точностью: достаточно выбирать крест, в котором цетральная подматрица будет иметь максимальный объем среди всех подматриц такого же размера. Принцип появился в ИВМ РАН и недавно получил новое развитие в связи с различными обобщениями понятия объема матрицы. К простейшему методу оптимизации функционала от многих переменных относится, конечно, метод последовательной координатной оптимизации. При этом координаты можно объединять в блоки и последовательно оптимизировать по блокам. Цель исследования – построить метод выбора блока, основанный на принципе максимального объема, и, возможно, получить новые эффективные методы оптимизации.
Часто решение задачи ищется в виде разложения по заданному базису, и заметим, что заведомо существуют базисы, для которых вектор коэффициентов разложения оказывается разреженным. За последние 10-15 лет очень интенсивно развивалось новое научное направление, связанное с поиском разреженных или приближенно разреженных решений, в том числе в задачах линейной алгебры. Здесь сложность заключается прежде всего в том, что неизвестно, какие именно коэффициенты будут ненулевыми. Как выбрать базис, гарантирующий разреженность? Конечно, идеальная ситуация – когда базис содержит искомое решение. Но решение – это как раз то, что мы ищем! Цель исследования – понять, как можно находить разрежающие базисы в задачах математической физики, прежде всего для интегральных уравнений теории потенциала. Есть надежда, что в результате получатся совершенно новые эффективные методы решения многих практически важных задач. |
|
Моделирование климатаНаучный руководитель д.ф.-м.н. Володин Е.М., комната 612, e-mail: volodinev at gmail.com, Понимание механизмов формирования современного климата, а также прогноз его изменений в будущем, представляет собой ключевую задачу современной науки. В настоящее время, одним из основных методов исследований в данной области является математическое моделирование со все более полным учетом всех факторов, влияющих на климатическую систему. При этом в задачах прогноза состояния климатической системы моделирование является, по сути, единственным возможным методом получения практически востребованного результата. Консолидация мировых усилий в данном направлении осуществляется в рамках программы сравнения климатических моделей CMIP (https://www.wcrp-climate.org/wgcm-cmip), в которой участвуют все ведущие климатические центры и, в том числе, ИВМ РАН с моделями семейства INMCM (Volodin et al., ClimDyn, 2016). В рамках данного направления предлагается принять участие в следующих исследованиях. 1. Прогнозирование сезонных аномалий погоды. В настоящее время активно развивается направление сезонного прогноза аномалий погоды с помощью климатической модели ИВМ РАН, включающей в себя блоки атмосферы, океана и морского льда. Основными направлениями исследования являются выбор оптимальной конфигурации модели, способ задания начальных условий, разработка методов усвоения данных наблюдений и методов верификации прогнозов. 2. Прогнозирование декадных (десятилетних) аномалий климата. Прогноз естественных колебаний климата на временном масштабе порядка десятилетия с помощью климатической модели является новой интересной задачей. Такой прогноз возможен благодаря существованию в системе океан – атмосфера долгопериодных естественных колебаний с временными масштабами 10-50лет. Основными направлениями работы являются исследование природы естественных колебаний климата, способы подготовки начальных данных и выбор конфигурации модели, наиболее точно описывающей механизмы этих колебаний. 3. Прогноз вероятности экстремальных климатических аномалий. Прогноз экстремальных природно-климатических явлений (аномальных осадков, температур, ветров) (далее ЭЯ) на климатических временных масштабах (от года и до нескольких десятилетий) является важной научной проблемой, имеющей ярко выраженное экономическое значение. Поскольку рассматриваемые временные масштабы, очевидно, находятся за пределами возможностей детерминистического прогноза погоды, то «прогноз» здесь подразумевается в вероятностном (климатическом) смысле – предсказывается вероятность того или иного ЭЯ в заданном регионе. Основные направления исследований: оценка естественной (при отсутствии каких-либо воздействий на климатическую систему) вероятности числа и величины ЭЯ; выявление связей между статистическими характеристиками ЭЯ и модами естественной изменчивости климатической системы на различных временных масштабах; оценка величины трендов числа и величины ЭЯ в 20-21 веке по данным моделирования и наблюдений. |
|
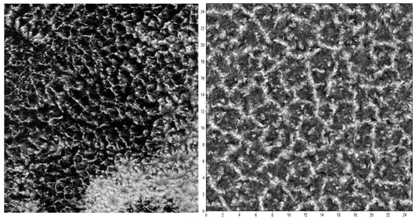
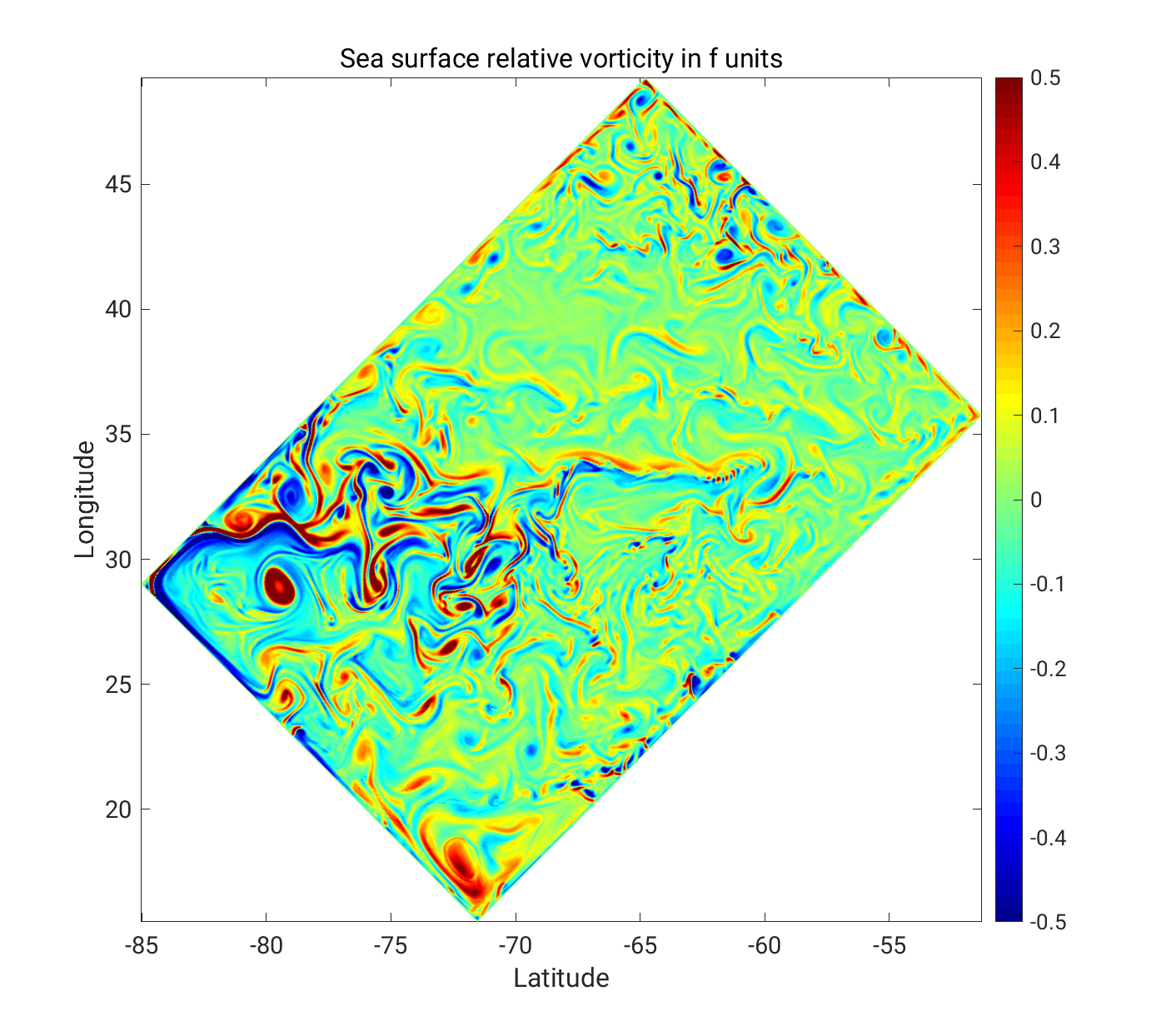
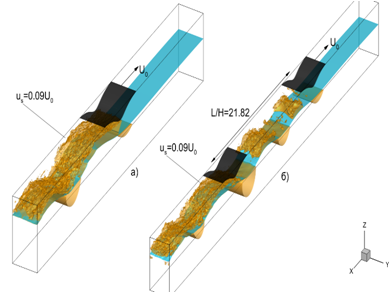
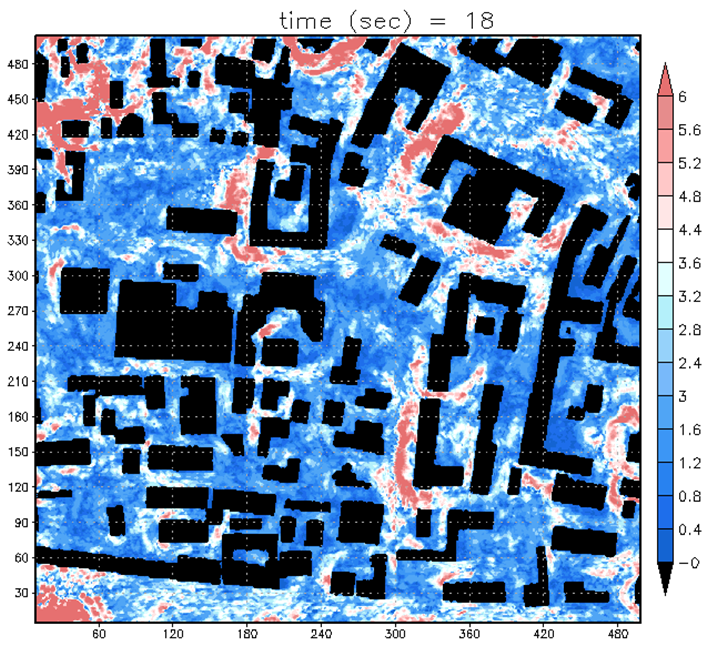
Численное моделирование геофизической турбулентностиНаучный руководитель д.ф.-м.н. Глазунов Андрей Васильевич, комната 607, email: and.glas at gmail.com Объектами изучения являются мелкомасштабная трехмерная стратифицированная турбулентность в пограничных слоях атмосферы и океана и крупномасштабная квазидвумерная турбулентность в геофизических средах. Студентам предлагается принять участие в исследованиях фундаментальных свойств турбулентных течений различной природы и в разработке новых численных моделей этих течений. Цели работ: 1. разработка и уточнение моделей взаимодействия подсеточной турбулентности и крупномасштабной циркуляции атмосферы и океана для включения в глобальные модели климата и прогноза погоды; 2. разработка численных моделей турбулентных течений в городской среде; 3. разработка моделей турбулентного переноса и дисперсии примесей в турбулентных течениях. Работы по теме направления включают: 1. проведение длительных расчетов на параллельных суперкомпьютерах с нестационарными гидродинамическими моделями высокого пространственного разрешения (прямое численное моделирование – Direct Numerical Simulation (DNS) и моделирование методом крупных вихрей – Large Eddy Simulation (LES)); 2. статистический анализ больших массивов данных численного моделирования и реализацию методов этого анализа; 3. модификацию численных моделей, как для постановки идеализированных численных экспериментов в исследовательских целях , так и для решения практических задач (например, для расчетов турбулентности в городской среде); 4. физическую интерпретацию результатов расчетов с моделями высокого пространственного разрешения и построение упрощенных математических моделей и параметризаций обнаруженных эффектов. |
    |
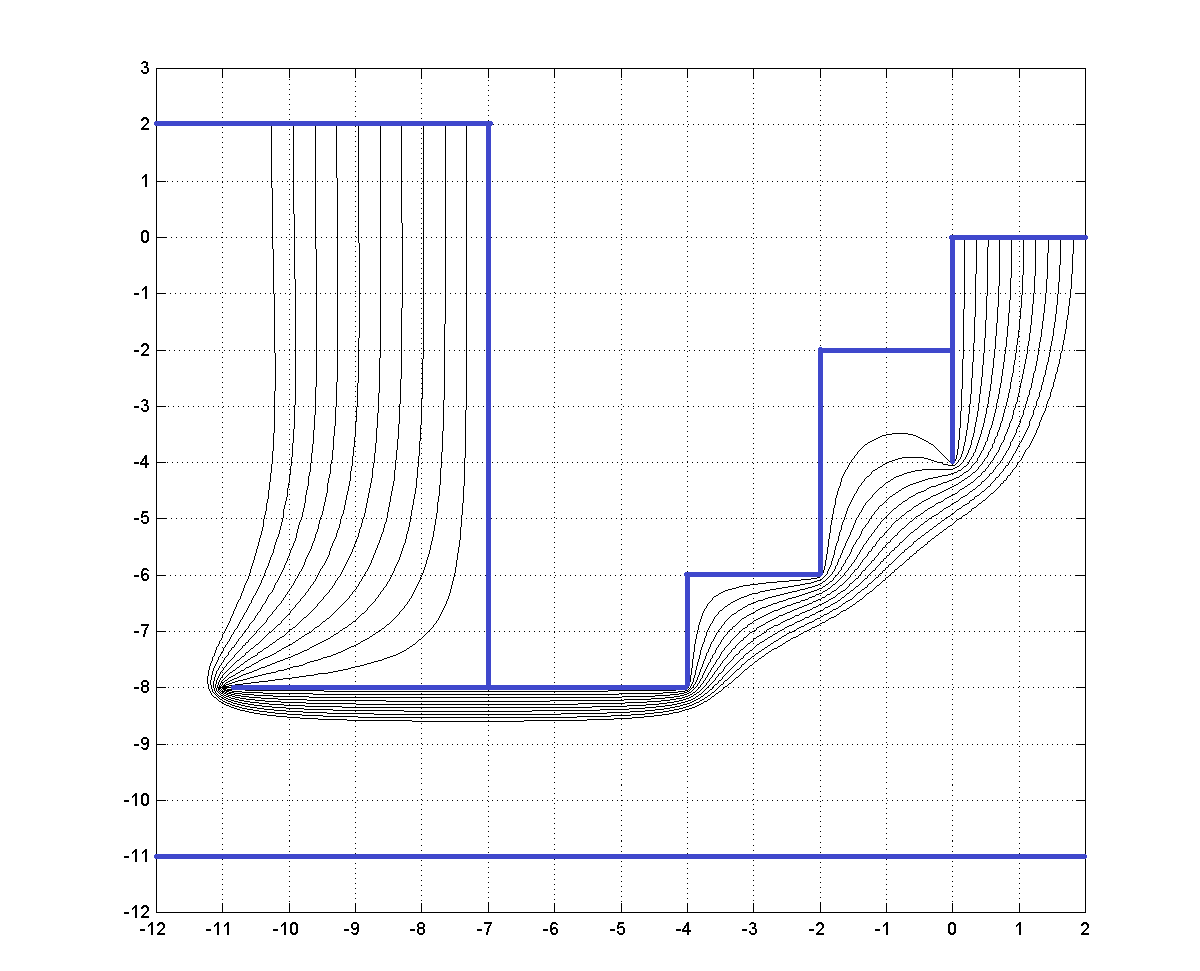
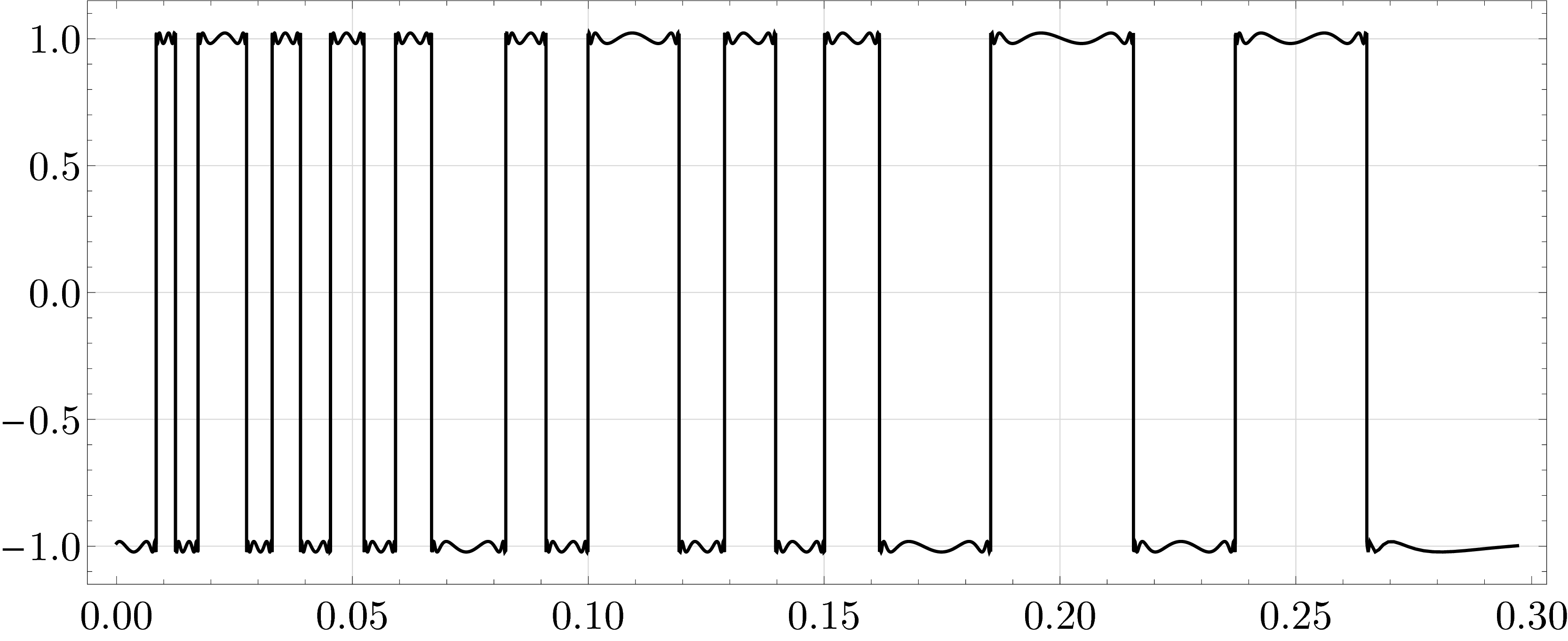
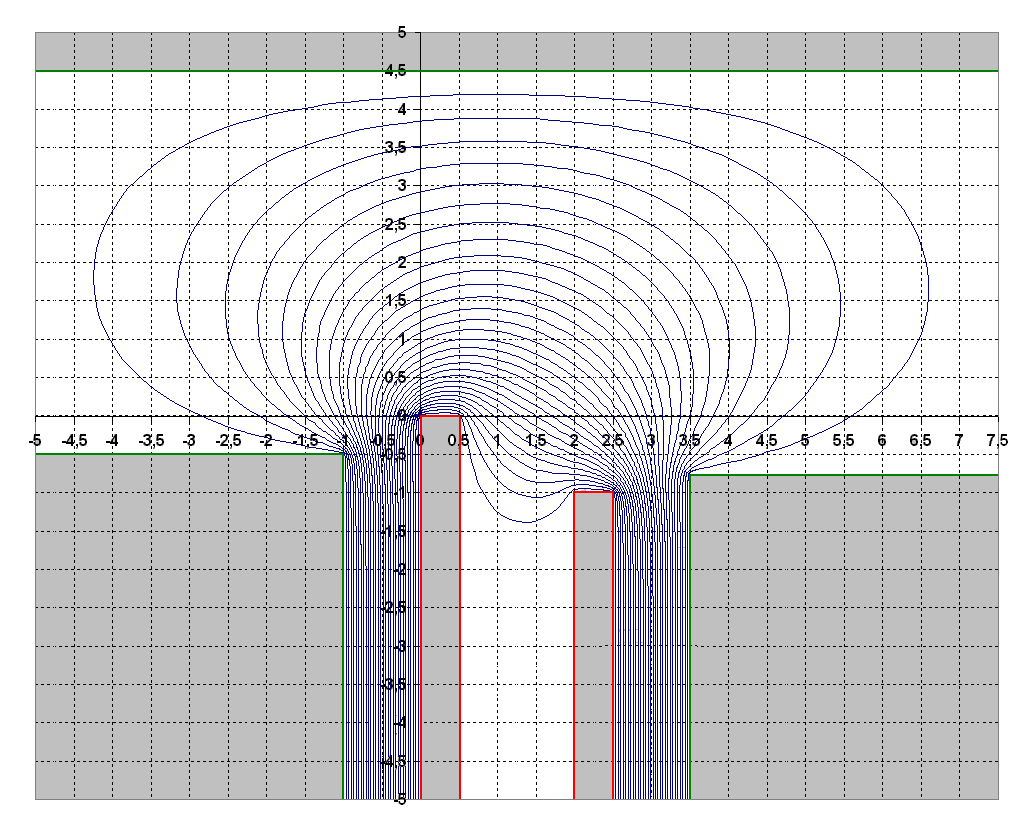
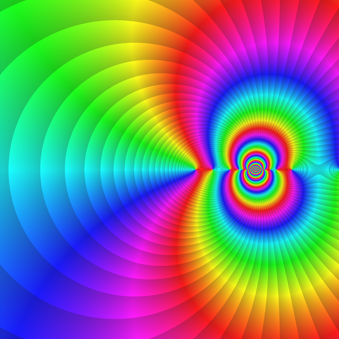
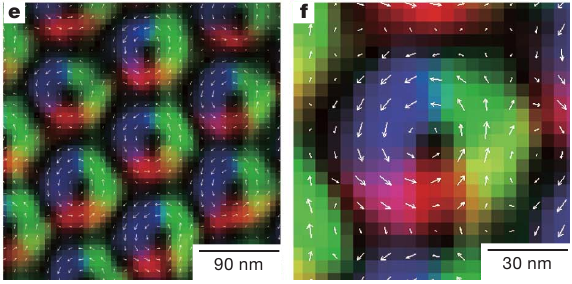
Экспериментальная математикаНаучный руководитель д.ф.-м.н. Богатырев А.Б., комната 616 (615), ab.bogatyrev at gmail.com Вот несколько конкретных направлений для разработки оптимальных методов, в которых могут возникать студенческие проекты, прежде всего как “экспериментальная математика” и работа с программным кодом; есть много места и для глубокой теории. 1. Рациональная аппроксимация и оптимизация в равномерной метрике. Теоремы об альтернативах имеют прямое применение в задачах о наименьшем отклонении в Чебышевской метрике; геометрические аналогии помогают здесь и при построении алгоритмов, и при анализе сходимости. Конкретным приложением (ощутимо поддерживаемым компанией Хуавей) является расчет и настройка многополосных электрическихфильтров (аналоговых, цифровых и СВЧ). 2. Алгебро-геометрический подход к построению фильтров: Оказывается, что привлечение римановых поверхностей высоких родов позволяет решить задачу о наименьшем отклонении от идеальной функции пропускания в виде явных аналитических формул. Предлагается исследовать модификации получаемого алгоритма. Для эффективной реализации теории функций на Римановых поверхностях и пространствах их модулей используются несколько подходов: теория тэта функций Римана, родственных им сигма функций (Вейерштрасса и Кляйна), а также ряды Пуанкаре. Предлагается исследовать устойчивость рекуррентных соотношений, задающих ряды для сигма функций. 3. Ускорение сходимости тэта-рядов Пуанкаре: представления римановых поверхностей допускающих отражение в виде орбит группы Шоттки обладают важным практическим свойством: линейные ряды Пуанкаре для такой группы сходятся абсолютно. Для практических применений таких рядов, к которым относится, например, описание магнитных состояний планарных магнитов субмикронных размеров, бывает важно преобразовывать эти ряды с целью ускорения их сходимости; первые примеры таких преобразований уже реализованы. 4. Построение конформных сеток: Для плоских областей нарисованных по линиям миллиметровки, рассматриваемых как канал, по которому течет идеальная жидкость, требуется рассчитать поля скоростей и давления. Оказывается, что такая задача имеет аналитическое решение в терминах тэта-функций и решается с машинной точностью равномерно во всей области. Предлагается использовать такое решения для тестирования других численных методов, использующих сеточные аппроксимации. Приближения Каратеодори-Фейера: это конструкция, позволяющая приближенно решать задачи о наименьшем отклонении с весом сведением к задаче на собственные значения специальной матрицы с ганкелевой структурой. Предлагается исследовать обоснование классического метода КФ и его обобщения для неодносвязных областей. Конструкция Пенроуза: так называемое твисторное соответствие лежит в основе представления компонент электрического и магнитного полей в виде контурных интегралов от произвольных функций на пространстве твисторов с заданными степенями однородности. Предлагается получать явные представления решений уравнений Максвелла в простых областях (потребуется знакомство с теорией Пенроуза). Вложенные рассечения: Оптимальное упорядочение неизвестных при гауссовом исключении есть NP-полная задача. В частных случаях (например, задача Дирихле в двумерном случае) существует некоторая иерархическая конструкция, известная как метод вложенных рассечений, которая такое упорядочение позволяет найти. Предлагается исследовать некоторые обобщения (потребуется знакомство с теорией графов и дискретной дифференциальной геометрией). Оптимизация параметров многосеточных методов: Некоторые прямые методы решения линейных систем допускают интерпретацию в виде метода из семейства многосеточных (изобретенных Р. П. Федоренко). Использование этой связи оказывается весьма продуктивным для обеих сторон. В качестве приложений можно рассматривать задачи квазимагнитостатики. |
     |
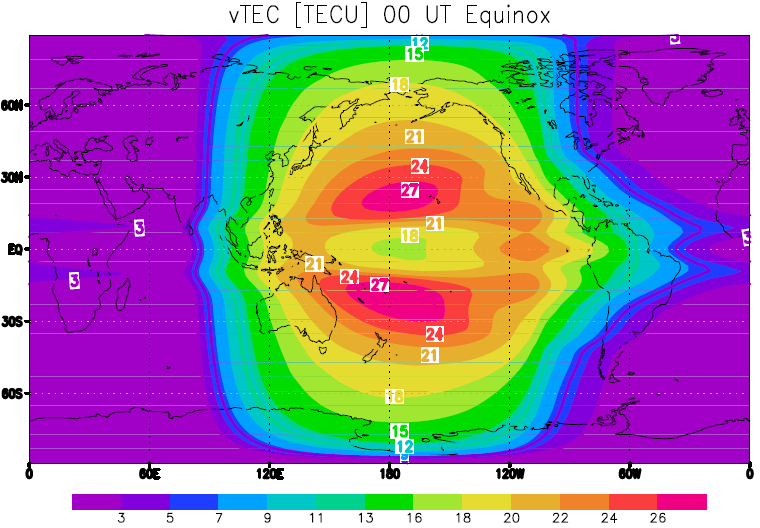
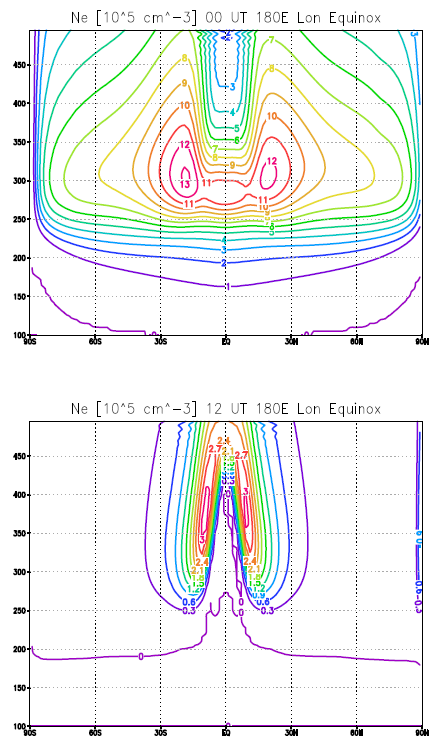
Математическое моделирование верхней атмосферы и ионосферы ЗемлиНаучный руководитель к.ф.-м.н. Кулямин Д.В., комната 608, kulyamind at mail.ru Тема исследований Ключевой задачей научной группы является разработка глобальной модели общей циркуляции атмосферы (для 0-500 км) с включением описания ионосферы и воздействия космических факторов на формирование состояния атмосферы Земли на различных высотах. Подобная модель позволит по-новому взглянуть на ряд проблем, связанных с влиянием космических факторов на климат Земли, солнечно-земными связями и взаимодействием Земной и космической погоды. Основные проблемы моделирования верхней атмосферы связаны как с построением и реализацией эффективных и устойчивых численных алгоритмов для решения основных уравнений моделей различного типа, так и с исследованием с помощью разрабатываемых моделей и анализа данных наблюдений ключевых физических процессов, ответственных за формирование глобального состояния и изменчивости среды, в том числе с анализом связей верхних и нижних слоев. Отдельной проблемой является использование данных наблюдений о верхней атмосфере и ионосфере для усовершенствования и анализа результатов модели, а также решения задачи прогноза, что включает построение специальных параметризаций, систем усвоения данных, а также использование нейронных сетей. Предлагаемые задачи 1. Разработка гидродинамического вычислительного ядра для полной глобальной модели общей циркуляции атмосферы (для высот 0-500 км). Задача предполагает создание и реализацию эффективного и устойчивого алгоритма решения уравнений гидротермодинамики атмосферы для слоя с высокой верхней границей в качестве основы перспективной модели Земной системы на основе существующих разработок и моделей атмосферы ИВМ РАН. Ключевые проблемы данной задачи состоят в значительном изменении с высотой основных параметров среды (атмосферное давление падает на 15 порядков, температура растет в 3-6 раз) и поиске обоснованных математических методов моделирования динамики всей атмосферы при условии правильного описания физики основных глобальных процессов на разных высотах. 2. Разработка параметризаций физических процессов для моделей верхней атмосферы: волновых процессов и их воздействия на общую циркуляцию, электромагнитных процессов и их роли в динамики ионосферы, и др. Данные параметризации будут основой описания физических явлений в разрабатываемой полной модели атмосферы (0-500 км) Предполагается использование как детерминированных физических приближений, так и динамико-стохастических подходов. Решение данной задачи требует детального исследования физики отдельных процессов и правильного описания их влияния на глобальную термодинамику атмосферы и ионосферы в рамках модели общей циркуляции. 3. Разработка системы усвоения данных для модели ионосферы и верхней атмосферы на основе вариационной ассимиляции для решения задачи прогноза состояния Земной ионосферы. Данная задача является крайне актуальной прикладной задачей прежде всего для описания состояния ионосферы в связи с ее важностью для спутниковой радиосвязи и других проблем при освоении околоземного космического пространства. Решение задачи требует аналитической и программной разработки глобальной для Земли согласованной системы усвоения на основе разрабатываемой коллективом модели ионосферы и атмосферы и рядов данных мировых наблюдений за состоянием ионосферы (главным образом, данные о полном электронном содержании, а также данные о профилях электронной плотности в разных точках) 4. Разработка и реализация нейронной сети для усвоения данных наблюдений и прогноза состояния Земной ионосферы. Предлагаемый подход является полностью новым и состоит в задаче построения обучаемой нейронной сети для моделирования отклика состояния ионосферы на различные схожие внешние воздействия (такие как геомагнитные бури, Солнечные вспышки и усиления космического излучения и др.) 5. Построение оператора отклика ионосферы на малые внешние воздействия на основе данных наблюдений и моделирования с использованием динамико-стохастических подходов. Подобная задача по существу направлена на использование специальных методов по анализу и оценке откликов динамических сред на малые возмущения, разработанных в ИВМ РАН, в применении к верхней атмосфере и ионосфере Земли. |
  |